误差运动学计算的一些笔记-PID控制

参考资料：现代机器人学

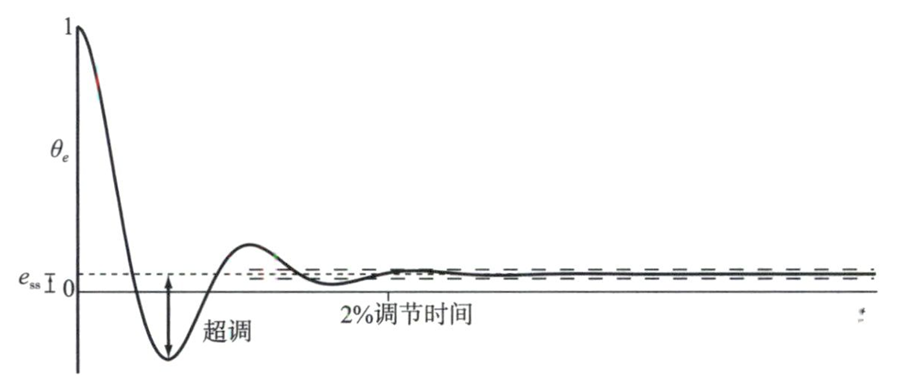
• 态误差很小或者为零
• 超调很小或者零超调
• 2％调节时间很短 \(\left|\theta_{e}(t)-e_{\mathrm{ss}}\right| \leqslant 0.02\left(\theta_{e}(0)-e_{\mathrm{ss}}\right)\)

对于二阶误差动力学，我们要记住的—个非常好的机械类比是：线性的质量-弹簧—阻尼系统!!!

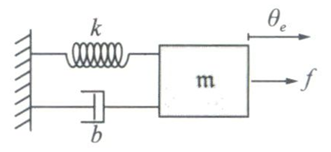
\(m\ddot{\theta}_e + b\dot{\theta}_e + k\theta_e = f\)

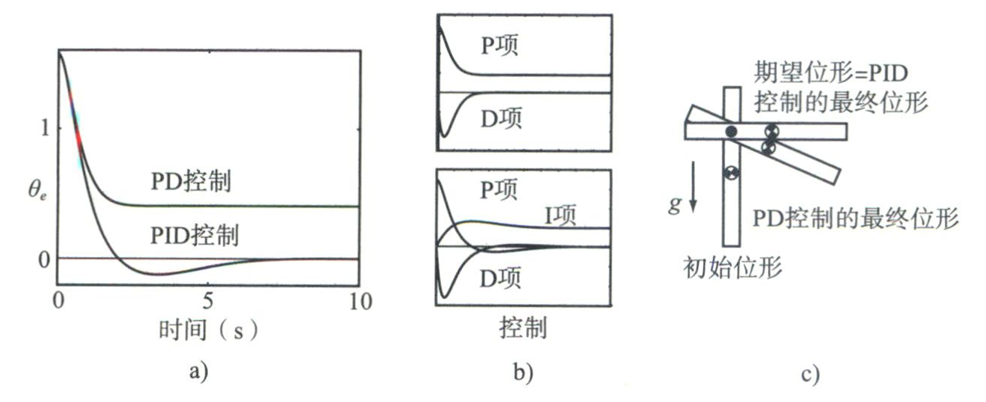
\(\tau = K_p \theta_e + K_i \int \theta_e(t) \, dt + K_d \dot{\theta}_e\)

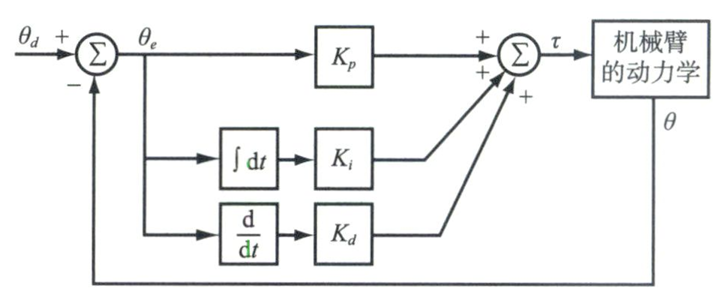
PID 控制器实现

type PIDConfig = {
    Kp: float // 比例
    Ki: float // 积分
    Kd: float // 微分
    MinOutput: float
    MaxOutput: float
}

type PIDState = { IntegralSum: float; PrevError: float }

let calculatePID (config: PIDConfig) (state: PIDState) target current dt =
    let error = target - current

    let pOut = config.Kp * error

    let newIntegral = state.IntegralSum + (error * dt)
    let iOut = config.Ki * newIntegral

    let derivative = (error - state.PrevError) / dt
    let dOut = config.Kd * derivative

    let rawOutput = pOut + iOut + dOut

    let output = Math.Clamp(rawOutput, config.MinOutput, config.MaxOutput)
    let newState = { IntegralSum = newIntegral; PrevError = error }

    output, newState

汽车速度控制模型

// F = ma  ->  a = F/m
// v = v + (a * time)
type CarState = {
    Mass: float // kg
    Velocity: float // m/s
    DragCoeff: float // 空气阻力系数
}

let calculateCarState (car: CarState) forceApplied dt =
    // 空气阻力与速度成正比
    let dragForce = car.Velocity * car.DragCoeff

    let netForce = forceApplied - dragForce
    let acceleration = netForce / car.Mass

    { car with Velocity = car.Velocity + acceleration * dt }

let simulate (pidConfig: PIDConfig) =
    let mutable pidState = { IntegralSum = 0.0; PrevError = 0.0 }
    let mutable carState = { Velocity = 0.0; Mass = 1000.0; DragCoeff = 50.0 }

    let dt = 0.1 // 时间步长（秒）
    let targetVelocity = 10.0
    let simulationDuration = 150.0 // 秒

    let times = ResizeArray<float>()
    let velocities = ResizeArray<float>()
    let targetVelocities = ResizeArray<float>()

    let mutable maxError = 0.0
    let mutable p2Time = ValueNone

    for i in 0 .. int (simulationDuration / dt) do
        let engineForce, newPidState = calculatePID pidConfig pidState targetVelocity carState.Velocity dt
        let newCarState = calculateCarState carState engineForce dt
        let error = Math.Abs(targetVelocity - carState.Velocity)

        times.Add(float i * dt)
        velocities.Add(newCarState.Velocity)
        targetVelocities.Add(targetVelocity)

        pidState <- newPidState
        carState <- newCarState
        if error > maxError then maxError <- error
        if p2Time.IsNone && error <= 0.02 * targetVelocity then
            p2Time <- ValueSome(float i * dt)

    printfn $"> 最大误差: {maxError:F0} m/s, 2%%调节时间: {p2Time |> ValueOption.defaultValue simulationDuration:F0} 秒"
    printfn ""
    printChart $"汽车速度模拟PID控制-{pidConfig.Kp}_{pidConfig.Ki}_{pidConfig.Kd}" [
        {| Name = "实际速度"; XY = Seq.zip times velocities |}
        {| Name = "目标速度"; XY = Seq.zip times targetVelocities |}
    ]

模拟1

simulate {
    Kp = 100.0 // 尝试 5.0（慢）与 200.0（激进）
    Ki = 5.0 // 尝试 0.0（将定义稳态误差）
    Kd = 10.0 // 尝试 0.0 与 50.0（阻尼振荡）
    MinOutput = 0.0 // 不能施加负油门
    MaxOutput = 5000.0 // 最大发动机力
}

最大误差: 10 m/s, 2%调节时间: 39 秒

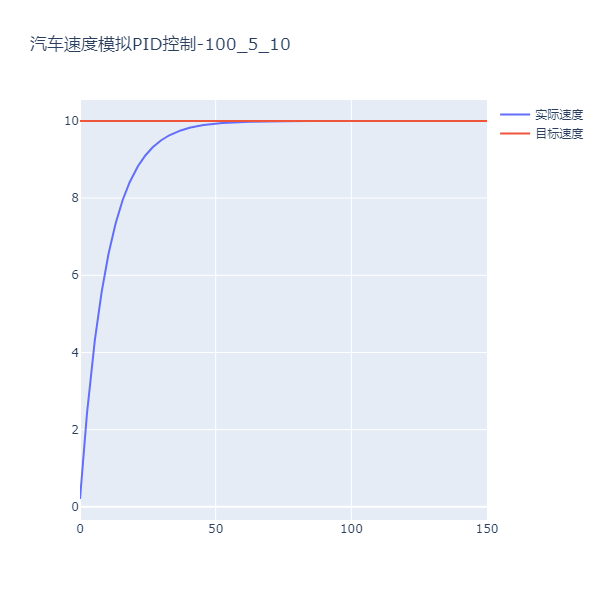
模拟2

// 当积分项为0，变为 PD 控制器，稳态误差则无法消除。但是可以通过前馈控制来补偿稳态误差。
simulate {
    Kp = 500.0
    Ki = 0
    Kd = 100.0
    MinOutput = 0.0
    MaxOutput = 5000.0
}

最大误差: 10 m/s, 2%调节时间: 150 秒

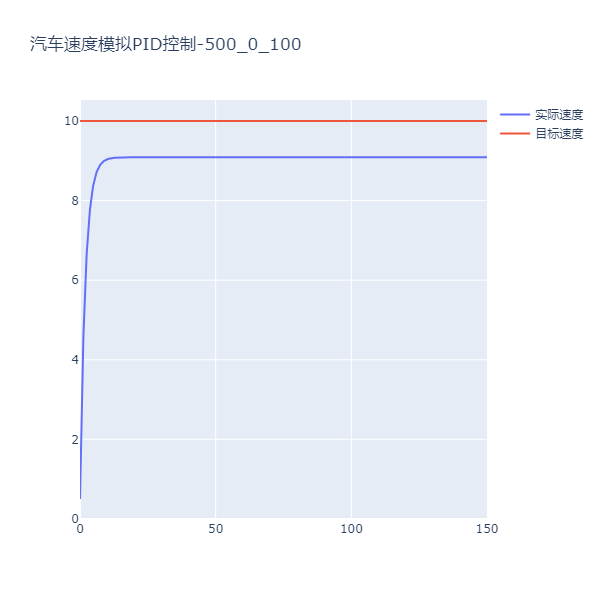
PID 控制器调参建议

通常的设计策略是：选取合适的Kp和Kd以获得良好的瞬态响应， 然后选择Ki，它要足够大以有助于减少或消除稳态误差，但又要小到足以使其不会显著影响稳定性。 相对较大的Ki会使瞬态响应变差，从而产生明显的超调，但它消除了稳态误差。

各个参数通俗意义的解释：

• Kp: 是对系统当前误差的即时反应。较高的Kp值会导致系统更快地响应误差，但过高可能引起系统振荡或不稳定。
• Ki: 是对过去误差的累积反应。它有助于消除稳态误差，但过高的Ki值可能导致系统过度反应，从而引起振荡。或不稳定。
• Kd: 是对未来误差（变化率）的反应。它有助于抑制系统的振荡，提供阻尼效果。过高的Kd值可能导致系统响应过慢。